Нечеткая логика

Введение

Математическая теория нечетких множеств (fuzzy sets) и нечеткая логика (fuzzy logic) являются обобщениями классической теории множеств и классической формальной логики. Данные понятия были впервые предложены американским ученым Лотфи Заде (Lotfi Zadeh) в 1965 г. Основной причиной появления новой теории стало наличие нечетких и приближенных рассуждений при описании человеком процессов, систем, объектов.

Прежде чем нечеткий подход к моделированию сложных систем получил признание во всем мире, прошло не одно десятилетие с момента зарождения теории нечетких множеств. И на этом пути развития нечетких систем принято выделять три периода.

Первый период (конец 60-х–начало 70 годов) характеризуется развитием теоретического аппарата нечетких множеств (Л. Заде, Э. Мамдани, Беллман). Во втором периоде (70–80-е годы) появляются первые практические результаты в области нечеткого управления сложными техническими системами (парогенератор с нечетким управлением)

Одновременно стало уделяться внимание вопросам построения экспертных систем, основанных на нечеткой логике, разработке нечетких контроллеров. Нечеткие экспертные системы для поддержки принятия решений находят широкое применение в медицине и экономике

Наконец, в третьем периоде, который длится с конца 80-х годов и продолжается в настоящее время, появляются пакеты программ для построения нечетких экспертных систем, а области применения нечеткой логики заметно расширяются. Она применяется в автомобильной, аэрокосмической и транспортной промышленности, в области изделий бытовой техники, в сфере финансов, анализа и принятия управленческих решений и многих других.

Триумфальное шествие нечеткой логики по миру началось после доказательства в конце 80-х Бартоломеем Коско знаменитой теоремы FAT (Fuzzy Approximation Theorem). В бизнесе и финансах нечеткая логика получила признание после того как в 1988 году экспертная система на основе нечетких правил для прогнозирования финансовых индикаторов единственная предсказала биржевой крах. И количество успешных фаззи-применений в настоящее время исчисляется тысячами.

Пример сортировки рыбы

Компания PiscesVMK производит технологическое оборудование для переработки рыбы на борту и на прибрежных заводах. Клиенты фирмы – рыбоперерабатывающие суда, выполняющие круглогодичный лов различных сортов рыбы в Северном море и Атлантическом океане. Эти потребители хотят заполнить свои трюмы как можно быстрее уловом наивысшего качества при минимальной численности работников.

Как правило, рыба доставляется на борт с помощью сетей и выгружается в емкости на конвейере, который переносит их через машины очистки, нарезки и филетирования. Возможные отклонения включают неподходящий сорт, повреждение рыбы, наличие больше одной рыбы в емкости и ее неправильное положение перед поступлением в машину нарезки. Реализация такого контроля традиционными средствами обработки изображений затруднена, поскольку размеры, форму и объем сложно описать математически. Кроме того, эти параметры могут меняться в зависимости от места плавания и сезона.

Pisces установила более 20 систем, базирующихся на интеллектуальной камере Iris от Matrox и механизме распознавания CogniSight от General Vision. Камера монтируется над конвейером так, чтобы рыба проходила под ней как раз перед попаданием в филетирующую машину. Камера связана с контроллером Siemens Simatic S7-224 (ПЛК) и с локальной сетью (LAN). Стробоскопический источник света, установленный рядом с камерой, запускается каждый раз, когда новая емкость появляется в поле зрения. Соединение камеры с локальной сетью необходимо для выполнения трех операций: настройки преобразователя, гарантирующей фокусировку и надлежащий контраст изображения, обучения механизма распознавания и доступа к статистике, непрерывно сообщающей о количестве кондиционной и некондиционной рыбы.

Лингвистические переменные

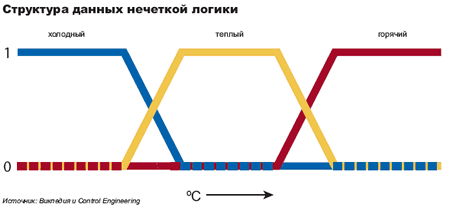
В нечеткой логике значения любой величины представляются не числами, а словами естественного языка и называются ТЕРМАМИ. Так, значением лингвистической переменной ДИСТАНЦИЯ являются термы ДАЛЕКО, БЛИЗКО и т. д.

Конечно, для реализации лингвистической переменной необходимо определить точные физические значения ее термов. Пусть, например, переменная ДИСТАНЦИЯ может принимать любое значение из диапазона от 0 до 60 метров. Как же нам поступить? Согласно положениям теории нечетких множеств, каждому значению расстояния из диапазона в 60 метров может быть поставлено в соответствие некоторое число, от нуля до единицы, которое определяет СТЕПЕНЬ ПРИНАДЛЕЖНОСТИ данного физического значения расстояния (допустим, 10 метров) к тому или иному терму лингвистической переменной ДИСТАНЦИЯ. В нашем случае расстоянию в 50 метров можно задать степень принадлежности к терму ДАЛЕКО, равную 0,85, а к терму БЛИЗКО — 0,15. Конкретное определение степени принадлежности возможно только при работе с экспертами. При обсуждении вопроса о термах лингвистической переменной интересно прикинуть, сколько всего термов в переменной необходимо для достаточно точного представления физической величины. В настоящее время сложилось мнение, что для большинства приложений достаточно 3-7 термов на каждую переменную. Минимальное значение числа термов вполне оправданно.Такое определение содержит два экстремальных значения (минимальное и максимальное) и среднее. Для большинства применений этого вполне достаточно. Что касается максимального количества термов, то оно не ограничено и зависит целиком от приложения и требуемой точности описания системы. Число же 7 обусловлено емкостью кратковременной памяти человека, в которой, по современным представлениям, может храниться до семи единиц информации.

В заключение дадим два совета, которые помогут в определении числа термов:

n исходите из стоящей перед вами задачи и необходимой точности описания, помните, что для большинства приложений вполне достаточно трех термов в переменной;
n составляемые нечеткие правила функционирования системы должны быть понятны, вы не должны испытывать существенных трудностей при их разработке; в противном случае, если не хватает словарного запаса в термах, следует увеличить их число.

Модели систем нечеткой логики

Простые системы нечеткой логики

Базовая конфигурация простой системы нечеткой логики представлена на Рисунке 8. Базис нечетких правил содержит набор нечетких IF-THEN (ЕСЛИ-TO) правил, а механизм нечеткого вывода на основе принципов нечеткой логики использует эти IF-THEN-правила для отображения нечетких множеств из входящего множества высказываний X{\displaystyle X \,\! } в нечеткие множества из множества высказываний Y{\displaystyle Y \,\! } на выходе системы. Нечеткие IF-THEN-правила выглядят следующим образом:

IFx1{\displaystyle IF\qquad x_1\,\! } есть F1p{\displaystyle F_{1^p}\,\! } и . . . и xn{\displaystyle x_n\,\! } есть FnpTHENy{\displaystyle F_{n^p}\qquad THEN\qquad y\,\! } есть Gp{\displaystyle G^p \,\! }

где Fip{\displaystyle F_{i^p} \,\! } и Gp{\displaystyle G^p \,\! } — нечеткие множества;

x¯=(x1,…,xn)T∈X{\displaystyle \bar{x}=(x_1,…,x_n)^T \in X \,\! } и y∈X{\displaystyle y \in X \,\! } есть входные и выходная лингвистические переменные соответственно;

p=1,m¯{\displaystyle p=\bar{1,m}\,\! }

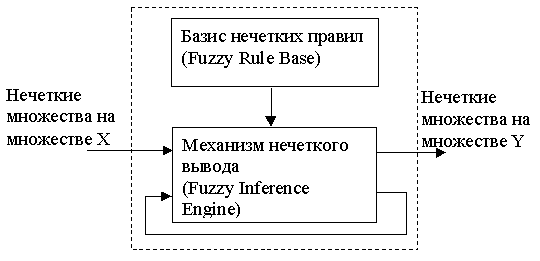
Рис. 7.1.1. Конфигурация простой системы нечеткой логики.

Практика показывает, что эти нечеткие IF-THEN-правила обеспечивают удобный механизм для представления знаний человека-эксперта. Каждое нечеткое IF-THEN-правило определяет нечеткое множество F1P×…×FnP→Gp{\displaystyle F_{1^P} \times …\times F_{n^P}\rightarrow G^p\,\! }

Структура простой системы нечеткой логики является существенной частью систем нечеткой логики. В общем случае, когда лингвистическая информация от эксперта переводится в количественные показатели, принципы нечеткой логики используются для систематизации информации. Главным недостатком простых систем нечеткой логики является то обстоятельство, что ее входы и выходы — нечеткие множества, тогда как в большинстве технических систем входы и выходы являются переменными, принимающими реальные значения.

Нечеткие системы Такаги и Суджено

Вместо рассмотрения нечетких IF-THEN-правил в виде (1) Такаги и Суджено предложили использовать следующие IF-THEN-правила:

IFx1{\displaystyle IF\qquad x_1\,\! } есть F1p{\displaystyle F_{1^p}\,\! } и . . . иxn{\displaystyle x_n\,\! } есть FnpTHENyp=Cp+C1px1+…+Cnpxn{\displaystyle F_{n^p} \qquad THEN \qquad y^p = C_{0^p} + C_{1^p} x_1 + … + C_{n^p} x_n\,\! }

где Fip{\displaystyle F_{i^p}\,\! } — нечеткие множества;

Сi{\displaystyle С_i\,\! } — параметры, принимающие реальные значения;

yp{\displaystyle y^p\,\! } — выход системы, соответствующий правилу Lp{\displaystyle L^{p}};

p=1,M¯{\displaystyle p=\bar{1,M} \,\! }

Таким образом, они рассматривали правила, у которых часть IF{\displaystyle IF\,\! } является нечеткой, но «четкой» является часть THEN, и выход является линейной комбинацией переменных на входе. Для входного вектора вещественных переменных x¯=(x1,…,xn)T{\displaystyle \bar{x}={(x_1, …, x_n)}^T \,\! } выходу(x¯){\displaystyle у(\bar{x})\,\! } нечеткой системы Такаги-Суджено есть взвешенное среднее от yp−х{\displaystyle y^p-х:\,\! }

y(x¯)=∑p=1Mwpyp∑p=1Mwp{\displaystyle y(\bar{x})=\frac {\sum_{p=1}^M w^p y^p } {\sum_{p=1}^M w^p}\,\! }

где вес wp{\displaystyle w^p\,\! } подразумевает обобщенную величину истинности при применении к входу правила L(p){\displaystyle L^(p)\,\! }

вычисляется как wp=∏i=1nμFip(xi){\displaystyle w^p=\prod_{i=1}^n \mu_{F_{i^p}}(x_i)\,\! }

Конфигурация нечеткой системы Такаги-Суджено представлена на Рисунке 9:

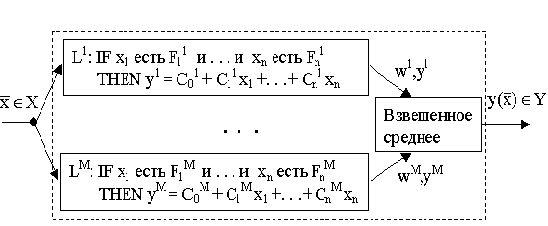
Рис. 7.2.1. Система нечеткой логики Такаги-Суджено.

Преимуществом систем нечеткой логики такого типа является то, что они описываются компактной системой уравнений. Для них могут быть легко разработаны методы оценки параметров и выбора порядка системы M{\displaystyle M}. Слабое место таких систем нечеткой логики заключается в том, что часть THEN в IF-THEN-правиле не является нечеткой, что не позволяет естественным образом получать нечеткие правила от человека-эксперта. Наибольшее распространение получили системы нечеткой логики с фаззификатором и дефаззификатором.

Синтез регулятора на базе нечеткой логики

Задаем симметричность функций, относительно нуля, тогда вместо двух чисел для максимума и минимума можно задать одно – Мах, и, соответственно диапазонно будет определен как [-Мах… Мах].
Задаем, равномерное распределение функций, тогда можно рассчитать положение всех вершин треугольников исходя из заданного диапазона.
Для трех функций координаты вершин определятся как –Max, 0, Max.
Задаем, что основание треугольника всех функций принадлежности одинаковы.

uMax(-uMax… uMax)deltaMax(-deltaMax… deltaMax)divMax(-divMax… divMax)div2Max(-div2Max… div2Max)uMax = 30deltaMax = 0.01divMax = 0.07div2Max = 1

Обзор

Нечеткая логика широко используется в управлении машинами. Термин «нечеткий» относится к тому факту, что задействованная логика может иметь дело с концепциями, которые не могут быть выражены как «истинные» или «ложные», а скорее как «частично истинные». Хотя альтернативные подходы, такие как генетические алгоритмы и нейронные сети, во многих случаях могут работать так же хорошо, как нечеткая логика, нечеткая логика имеет то преимущество, что решение проблемы может быть сформулировано в терминах, понятных операторам, так что их опыт может быть понят. использован в конструкции контроллера. Это упрощает механизацию задач, которые уже успешно выполняются людьми.

Постановка задачи

Рассмотрим синтез цифрового ПИД-регулятора и нечеткого регулятора для системы управления ракетой по углу атаки. Методом математического моделирования определим процессы в системе и дадим сравнительную оценку качества системы при использовании синтезированных регуляторов.
Приняв за выходную координату ракеты угол атаки: ,
а за входную координату угол поворота руля определим передаточную функцию ракеты в виде:, где: – коэффициент преобразования ракеты, – коэффициент демпфирования, – постоянная времени.
Здесь и далее «передаточная функция» используется не в строгом классическом определении, как отношение перобразований лапласа.
При исследовании системы управления предположим, что зависимости параметров ракеты от времени полета определяются так:
Для упрощения расчетов, рулевой механизм опишем передаточной функцией интегрирующего звена В этом случае вход системы — заданный угол атаки, выход системы — отработанный ракетой угол атаки, m(t) – управляющий сигнал на выходе регулятора, а объект управления описывается общей передаточной функцией:
(В объект управления включены аналоговые рулевой механизм и ракета).
Закон изменения входного воздействия задан полиномом:
Необходимо разработать регулятор, обеспечивающий отработку входного воздействия с помощью ПИД-регулятора и регулятора на базе нечеткой логики.
Осуществить подбор коэффициентов регуляторов.
Произвести сравнение переходного процесса с ПИД-регулятором и c регулятором на базе нечеткой логики.

Операции над нечеткими множествами

Пусть A{\displaystyle A\,\!} и B{\displaystyle B \,\! } — нечеткие множества на универсальном множестве E{\displaystyle E\,\!}. Говорят, что A{\displaystyle A\,\!} содержится в B{\displaystyle B \,\! }, если∀x∈EAμ(x)≤Bμ(x){\displaystyle \forall x \in E \qquad A\mu(x)\le B\mu(x)\,\! } . Обозначение: A⊂B{\displaystyle A\subset B \,\! } .
Равенство	A{\displaystyle A\,\!} и B{\displaystyle B \,\! } равны, ∀x∈EAμ(x)=Bμ(x){\displaystyle \forall x \in E \qquad A\mu(x)=B\mu(x)\,\! } . Обозначение: A=B{\displaystyle A=B \,\! } .
Дополнение.	Пусть M=,1{\displaystyle M = \,\! }, A{\displaystyle A\,\!} и B{\displaystyle B \,\! }- нечеткие множества, заданные наE{\displaystyle E\,\!}. A{\displaystyle A\,\!} и B{\displaystyle B \,\! } дополняют друг друга, ∀x∈EAμ(x)=1−Bμ(x){\displaystyle \forall x \in E \qquad A\mu(x)=1- B\mu(x)\,\! } . Обозначение: A¯{\displaystyle \bar{A} \,\! } .
Пересечение	A∩B{\displaystyle A\cap B \,\! } — наибольшее нечеткое подмножество, которое содержится одновременно в A{\displaystyle A\,\!} и B{\displaystyle B \,\! }. Функция принадлежности: μA∩B(x)=min(μA(x),μB(x)){\displaystyle \mu A\cap B(x)=min(\mu A(x),\mu B(x))\,\! } .
Объединение	A∪B{\displaystyle A\cup B \,\! } — наименьшее нечеткое подмножество, которое включает какA{\displaystyle A\,\!}, так и B{\displaystyle B \,\! }, с функцией принадлежности: μA∪B(x)=max(μA(x),μB(x)){\displaystyle \mu A\cup B(x)=max(\mu A(x),\mu B(x))\,\! } .
Разность	A−B=A∩B¯(x){\displaystyle A-B=A\cap\bar{B}(x) \,\! } с функцией принадлежности:μA−B(x)=μA∪B¯(x)=min(μA(x),1−μB(x)){\displaystyle \mu A-B(x)=\mu A\cup\bar{B}(x)= min(\mu A(x),1-\mu B(x))\,\! }
Дизъюнктивная сумма	A∙B=(A−B)∪(B−A)=(A∩B¯)∪(B∩A¯){\displaystyle A\bullet B=(A-B)\cup(B-A)=(A\cap\bar{B})\cup(B\cap\bar{A}) \,\! } с функцией принадлежности: μA∙B(x)=max(min(μA(x),1−μB(x)),min(μB(x),1−μA(x))){\displaystyle \mu A \bullet B(x)=max(min(\mu A(x),1-\mu B(x)),min(\mu B(x),1-\mu A(x)))\,\! }

Ниже проиллюстрировано графическое представление операций над нечеткими множествами.

Пусть A{\displaystyle A\,\!} — нечеткий интервал между 5 до 8 и B нечеткое число около 4, как показано на рисунке.

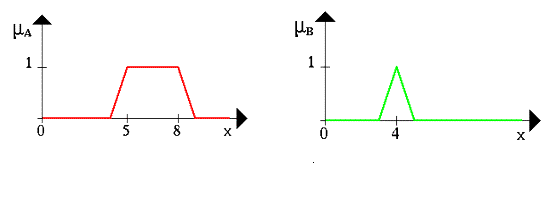
Рис. 3.1. Примеры характеристических функций нечеткого интервала и нечеткого числа.

Проиллюстрируем нечеткое множество между 5 и 8 И (AND) около 4 (жирная линия) на рисунке 3.2. Нечеткое множество между 5 и 8 ИЛИ (OR) около 4 показано на рисунке справа (снова жирная линия). Рисунок 3.3 иллюстрирует операцию отрицания. Жирная линия — это ОТРИЦАНИЕ нечеткого множества A{\displaystyle A\,\!}.

Обобщения

После обучения на примерах нейронная сеть способна к обобщению и может классифицировать ситуации, никогда ранее не наблюдавшиеся, связывая их со схожими ситуациям из примеров. С другой стороны, если система склонна к излишней свободе и обобщению ситуаций, ее поведение в любое время может быть скорректировано за счет обучения противоположным примерам.

С точки зрения нейронной сети эта операция заключается в уменьшении областей влияния существующих нейронов для согласования с новыми примерами, которые находятся в противоречии с существующим отображением пространства решений.

Важным фактором, определяющим признание ИНС, является самостоятельное и адаптивное обучение. Это означает, что устройство должно обладать способностью изучать объект с минимальным участием оператора или вообще без его вмешательства. В будущем, например, куклы, могли бы узнавать лицо ребенка, разворачивающего их впервые, и спрашивать его имя. Самостоятельное обучение для сотового телефона могло бы заключаться в изучении отпечатка пальца его первого владельца. Идентификация владельца также может быть усилена за счет совмещения в одном устройстве распознавания лица, отпечатка пальца и речи.

В условиях самостоятельного обучения устройство должно строить свой собственный механизм распознавания, который будет лучше всего функционировать в его рабочей среде. Например, интеллектуальная кукла должна распознать своего первоначального владельца независимо от цвета его волос и кожи, местонахождения или времени года.

На первых порах механизм должен использовать все методики выделения признаков, которые он знает. Это приведет к формированию ряда промежуточных механизмов, каждый из которых предназначен для идентификации тех же самых категорий объектов, но основан на наблюдении различных особенностей (цвет, зернистость, контраст, толщина границ и т.д.). После этого общий механизм может дать оценку работе промежуточных механизмов, выбирая те из них, которые дают лучшую производительность и/или точность.

Нечёткие числа

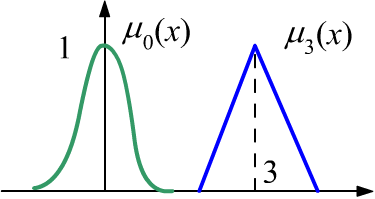
Нечёткое число $X$ — это функция принадлежности $\mu_X(x)$ от вещественного числа $x$,
имеющая единственный единичный максимум при $x=X$. На рисунке справа $\mu_0(x)$ —
это «примерно ноль», а $\mu_3(x)$ — примерно три.

Пусть есть вещественная функция двух (обычных) чисел $z=f(x,y)$
и два нечётких числа $A(x), B(y)$.
Нас интересует функция принадлежности $\mu_{f(A,B)}(z)$, равная степени уверенности
в том, что конкретное число $z$ является результатом операции (функции) $f$.

Переберём все возможные значения $x,y$ для которых $z=f(x,y)$
и выясним степени уверенности того, что это нечёткие числа $A(x), B(y)$.
Тогда по принципу расширения Заде функция принадлежности операции,
по определению, будет равна:
$$
\mu_{f(A,B)}(z) = \sup_{x,y: f(x,y)=z}\min\bigr\{\mu_A(x),\,\mu_B(y)\bigr\}.
$$
Таким образом, из всех возможных «чётких» способов получить $z$
выбираем то, которое даёт наибольшее ($\sup$) значение минимума функций принадлежности
нечётких чисел аргументов функции.

Часто для нечётких чисел используют функции принадлежности $L-R$ типа
$$
\mu_A(x) =
\left\{
\begin{array}{lll}
L(a-x) & x \ge a \\
R(x-a) & x \ge a \\
\end{array}
\right.
~~~~~~~
\begin{array}{lll}
L(0)=R(0) = 1 \\
L,R \text{ — не возрастают} \\
\end{array}
$$
Простейшим примером является треугольная функция принадлежности $\langle a;\, \alpha, \beta \rangle$, приведенная на рисунке.
При помощи принципа расширения для треугольных чисел
можно получить следующие результаты для стандартных арифметических операций:
$$
\begin{array}{lll}
\langle a_1;\, \alpha_1,\beta_1 \rangle \pm \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\pm a_2;\, \alpha_1+\alpha_2,\beta_1+\beta_2 \rangle\\
\langle a_1;\, \alpha_1,\beta_1 \rangle \cdot \langle a_2;\, \alpha_2,\beta_2 \rangle
= \langle a_1\cdot a_2;\, \alpha_1 a_2+\alpha_2 a_1,\beta_1 b_2+\beta_2 b_1\rangle\\
\langle a;\, \alpha,\beta \rangle^{-1} = \langle 1/a;\, \beta/a^2,\alpha/a^2 \rangle \\
\end{array}
$$
Обратм внимание, что для положения максимума выполняются обычные арифметические операции,
а величина нечёткости (ширина треугольника) увеличивается.

Другой способ задания функций принадлежности $\langle a,b; \alpha, \beta \rangle$ — это трапеция c максимумом на интервале $$
и граничными точками $\alpha,\beta$.

Возможно, вам также будет интересно

Smart Metering подразумевает установку интеллектуальных приборов учета на стороне потребителя, их регулярный опрос, обработку данных и предоставление информации о потреблении энергоресурсов.
Smart Grid – это управляемая сеть, осуществляющая сбор, обработку и распределение информации о потреблении ресурсов всеми участниками рынка с целью повысить эффективность, значимость, надежность, экономичн…

Технические усовершенствования и повышенная плотность установки серверов, а также усиленная нагрузка на имеющиеся мощности центров обработки данных привели к значительному увеличению тепловыделения. Дальнейшие разработки, такие как виртуализация и Cloud-приложения, предъявляют новые требования к ИТ-инфраструктуре. Компания Schroff предлагает новые модули мониторинга, помогающие эксплуатационникам центров обработки данных (ЦОД) контролировать критические параметры и удовлетворять основные требования к работе ЦОД.
Один раздел — это расширенный ассортимент панелей электропитания с измеряемыми …

Слово «инертность» в разговорной речи означает сопротивление изменениям и нежелание действовать. Едва ли это то, что нам нужно в инженерно-технической практике для разрешения насущных проблем, которые стоят перед нами. Даже в контексте системы движения идея придания инертности системе, то есть добавления механической массы, обычно нежелательна, так как это снижает скорость реакции системы. Одно…

Обработка изображений

С помощью принятия решений в ИНС, основанной на нечеткой логике, можно создать мощную систему управления. Очевидно, что две эти концепции хорошо работают вместе: алгоритм логического вывода с тремя нечеткими состояниями (например, холодный, теплый, горячий) мог бы быть реализован в аппаратном виде при использовании истинностных значений (0.8, 0.2, 0.0) в качестве входных значений для трех нейронов, каждый из которых представляет одно из трех множеств. Каждый нейрон обрабатывает входную величину в соответствии со своей функцией и получает выходное значение, которое далее будет входным значением для второго слоя нейронов, и т.д.

Например, нейрокомпьютер для обработки изображений может снять многочисленные ограничения по видеозаписи,освещению и настройкам аппаратуры. Такая степень свободы становится возможной благодаря тому, что нейронная сеть позволяет построить механизм распознавания с помощью изучения примеров. В результате система может быть обучена распознаванию годных и бракованных изделий при сильном и слабом освещении, при их расположении под разными углами и т.д. Механизм логического вывода начинает работать с“оценки”условий освещения (другими словами, устанавливает степень сходства с другими условиями освещения, при которых система знает, как действовать). После этого система выносит решение о содержании изображения используя критерии, основанные на данных условиях освещения. Поскольку система рассматривает условия освещения как нечеткие понятия, механизм логического вывода легко определяет новые условия по известным примерам.

Чем больше примеров изучает система, тем больший опыт приобретает механизм обработки изображений. Этот процесс обучения может быть достаточно легко автоматизирован, например, за счет предварительной сортировки по группам деталей с близкими свойствами для обучения по областям сходств и различий. Эти наблюдаемые сходства и различия могут далее предоставлять информацию ИНС, задача которой состоит в сортировке поступающих деталей по этим категориям. Таким образом, успех работы системы зависит не от стоимости оборудования, а от количества изображений, необходимых для обучения и построения надежного механизма логического вывода.

Нейрокомпьютер для обработки изображений подходит для приложений,где диагностика опирается на опыт и экспертную оценку оператора, а не на модели и алгоритмы. Процессор может построить механизм распознавания из простых комментариев к изображению, сделанных оператором, затем извлечь характеристики или векторы признаков из объектов, снабженных комментариями, и передать их в нейронную сеть. Векторы признаков, описывающие видимые объекты, могут быть такими простыми как значения строки пикселей, гистограмма или распределение интенсивности, профили распределения интенсивности или градиенты по соответствующим осям. Более сложные признаки могут включать элементы вейвлет-преобразования и быстрого преобразования Фурье.

В каких сферах применяют цифровые технологии?

Практически в любом бизнесе используют CRM, онлайн-сервисы для удаленной работы, хранения и работы с клиентской базой, управления бухгалтерией и товарного учета. Все больше компаний используют большие данные и аналитику, основанную на них, чтобы развивать бизнес и наращивать клиентскую базу.
В образовании используются гаджеты и программы для дистанционного обучения, подготовки и выполнения домашних заданий, составления презентаций, программирования и творческих задач. Виртуальная и дополненная реальность помогают лучше воспринимать материал и делают обучение более интерактивным. ИИ-алгоритмы помогают с профориентацией и учебным процессом.
В медицине цифровые технологии помогают быстрее находить новые лекарства и вакцины, точнее ставить диагноз даже на ранних стадиях, собирать аналитику для прогнозирования заболеваний, проводить онлайн-консультации и даже операции с применением AR и роботов.
В ретейле «цифра» упрощает процесс поиска и заказа товаров, управления складом и доставкой. Анализ поведения покупателей и данные о перемещении по торговым залам помогают оптимизировать пространство магазина. Голосовые помощники и чат-боты обрабатывают запросы с максимальной скоростью, а офлайновые магазины уже начинают работать без касс и продавцов — при помощи камер и алгоритмов распознавания лиц.
В сфере искусства и развлечений цифровые технологии открывают неограниченные возможности для игр, покупки и чтения книг, прослушивания музыки и просмотра Full HD видео онлайн, на стриминговых сервисах. Нейросети участвуют в создании музыки, живописи и книг, а виртуальные актеры и музыканты заменяют настоящих.
На производстве с помощью технологий автоматизируют отдельные линии и целые заводы, разрабатывают новые модели и материалы, следят за безопасностью и экологией, прогнозируют отказы оборудования, предотвращают брак и травмы, оптимизируют рабочее время и ресурсы.
В общепите цифровые технологии участвуют в сборе и распределении заказов, приготовлении блюд, контроле за количеством и сроками хранения продуктов и даже помогают находить новые точки с максимальным трафиком.

Топ-15 цифровых технологий по итогам 2020 года

Институт статистических исследований и экономики знаний (ИСИЭЗ) НИУ ВШЭ составил рейтинг самых перспективных цифровых технологий за 2020 год. В процессе подготовки эксперты использовали систему интеллектуального анализа больших данных iFORA, которая содержит более 500 млн документов: научные публикации, аналитика рынков, доклады международных организаций, правовые документы и др.

Топ-15 наиболее значимых технологий:

Глубокое обучение.
Сверточные нейросети.
Компьютерное зрение.
Обучение с подкреплением.
Обработка естественного языка.
Беспилотные автомобили.
Рекуррентные нейросети.
Трансферное обучение.
Генеративные состязательные сети.
Системы поддержки принятия решений.
Смарт-контракты.
Распознавание речи.
Квантовый компьютер.
Федеративное обучение.
Автономная робототехника.

Как видно из рейтинга, подавляющее большинство технологий имеет отношение к искусственному интеллекту, нейросетям и машинному обучению. Но это далеко не единственная сфера, которая определяет развитие технологий сегодня.

Логическая интерпретация нечеткого управления

Несмотря на внешний вид, есть несколько трудностей, чтобы дать строгую логическую интерпретацию правил IF-THEN . В качестве примера, интерпретируйте правило как ЕСЛИ (температура «холодная») ТОГДА (нагреватель «высокий») по формуле первого порядка Cold (x) → High (y) и предположите, что r — это вход, такой что Cold (r ) ложно. Тогда формула Cold (r) → High (t) верна для любого t и, следовательно, любое t дает правильный контроль при данном r . Строгое логическое обоснование нечеткого управления дано в книге Хайека (см. Главу 7), где нечеткое управление представлено как теория базовой логики Хайека.

В Gerla 2005 предлагается другой логический подход к нечеткому управлению, основанный на программировании с нечеткой логикой: Обозначим через f нечеткую функцию, возникающую из систем правил ЕСЛИ-ТО. Затем эту систему можно преобразовать в нечеткую программу P, содержащую серию правил с заголовком «Хорошо (x, y)». Интерпретация этого предиката в наименее нечеткой модели Эрбранда P совпадает с f. Это дает дополнительные полезные инструменты для нечеткого управления.

Логический вывод

В бинарной логике из $P$ логически следует $Q$,
если всегда, когда формула $P$ истинна, то истинна и формула $Q$.
Это обозначается так: $P\Rightarrow Q$.
Логический вывод — это способ получения одних истинных формул из других, также истинных.
Не стоит путать вывод и импликацию $P\to Q$, которая является логической связкой,
принимающая значения $0$ или $1$.

Рассмотрим простейший пример логического вывода: если истинна конъюнкция утверждений, то истинно (выводимо) каждое из утверждений.
В нечёткой логике это правило обобщается очевидным образом, приводя к интервальным оценкам
для выводимой формулы:
$$
A\,\&\,B~~~~~ \Rightarrow~~~~~~ A,~~~~~~~~~~~~~~~~~~~~~~\min(A,~B) ~~~\le~~~ A ~~~\le~~~ 1,
$$
где $\min(A,~B)$, с одной стороны является значением конъюнкции $A\,\&\,B$,
а с другой, нижней границей для $A$.
Естественно, в данном выводе предполагается, что степень истинности $A\,\&\,B$ задана
и в результате логического вывода, она ограничивает снизу значение истинности $A$.
Аналогично интерпретируются неравенства для следующего вывода:
$$
A~~~~~ \Rightarrow~~~~~~ A\vee B,~~~~~~~~~~~~~~~~~~~~~~0 ~~~\le~~~ A ~~~\le~~~ \max(A,~B).
$$

Таким образом, в нечёткой логике, по-мимо указания выводимой формулы,
необходимо уметь вычислять степень её истинности.
Определение такого логического вывода не вполне неоднозначно, что
отражено в многообразии предложенных двух высказываний.

Одна из возможностей, как и в вероятностной логике
считать, что $A~\Rightarrow~B$, если $A \le B$.
Примеры выводов, приведенные выше, удовлетворяют этому условию.
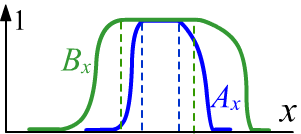
В случае предикатов, заданных на одном множестве
$\mathbb{X}$, такой вывод $A(x)~\Rightarrow~B(x)$ означает, что $A\subset B$ и множества $A,B$
являются нормальными, т.е. имеют единичную высоту (см. рисунок справа).
Тогда на срезе $\alpha=1$, $A$ будет обычным подмножеством $B$.

Часто знания (обыденные или математические) формулируют как правила «ЕСЛИ … TO …»
(импликация). Тогда в бинарной логике
важными методами вывода являются modus ponens и modus tollens
(запись посылок вывода через запятую подразумевает
связывание их логическим И):
$$
\begin{array}{cccccc}
A, & A\to B&~~~~~~~~&\Rightarrow&~~~~~~~~&B\\
\neg B,& A\to B&~~~~~~~~&\Rightarrow&~~~~~~~~&\neg A\\
\end{array}
$$
Считая эти выводы справедливыми в нечёткой логике,
найдём значения истинности получаемых формул.

Для modus ponens
имеем $\min(A,~A\to B) ~\le~ B~\le~ 1$. В случае когда «аксиома» $A \to B$ всегда истинна, то $A \le B$.
Если $A=1$, то $B=1$ (бинарный случай),
а при $A=0$ имеем $0 \le B\le 1$, т.е. значение $B$ полностью не определено
(что также согласуется с бинарной логикой).
Для modus tollens для истинного правила $A \to B$ также получаем
$$
A ~\le~ B ~\le~ 1.
$$
Напомним, что
получение значение истинности выводимых формул в виде неравенства
типично и для вероятностной логики.

Когда истинность правила $A\to B$ отлична от $1$, необходим выбор
той или иной формулы для импликации.
Отметим также, что из всех определений импликации с неравенством
$\min(A,~A\to B) \le B$ в общем случае согласуются только импликации Шарпа и Брауэра.

В бинарной логике существует очень мощный метод вывода по резолюции,
применяемый в машинном выводе:
$$
A\vee C,~\neg A\vee B~~~~~~~~~~\Rightarrow~~~~~~~~~~C\vee B.
$$
В нечёткой логике он не работает, т.к. неравенство
$\min\bigr(\max(A,C),~\max(1-A, B)\,\bigr)~\le \max(C,B)$
не является верным (например, для $A=1/2,~B=C=0$). Это связано с нарушением закона исключения третьего.
В бинарной логике резолюция означает, если
посылки истинны, то либо $A=0$ и тогда $C=1$, $B$ — любое,
либо $A=1$ и тогда $B=1$, $C$ — любое. Поэтому в любом случае $B \vee C$ истинно.